

Geometric sequence formula sn series#
So the infinite geometric series with common ratio |r| 1 can not have a finite sum. Sum of the first 'n' terms, S n = a(1-r n)/(1-r) when r ≠ 1.Here are the GP formulas for a geometric progression with the first term 'a' and the common ratio 'r': is a geometric progression as every term is getting multiplied by a fixed number 3 to get its next term.
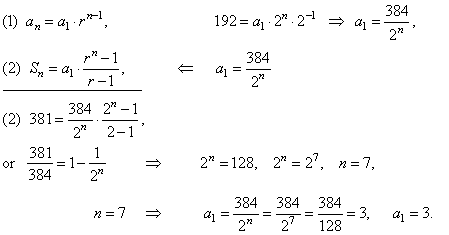
Geometric progressions are patterns where each term is multiplied by a constant to get its next term. The sum of infinite GP formula is given as: S n = a/(1-r) where |r|The sum of n terms in GP whose first term is a and the common ratio is r can be calculated using the formula: S n = / (1-r).The formula for the nth term of a geometric progression whose first term is a and common ratio is r is: a n=ar n-1.In a geometric progression, each successive term is obtained by multiplying the common ratio to its preceding term.Important Notes on Geometric Progression: The variation of the terms is non-linear. Here are a few differences between geometric progression and arithmetic progression shown in the table below: Geometric ProgressionĪP has the same common difference throughout.Ī new term is the product of the previous term and the common ratioĪ new term is the sum of the previous term and the common difference.Īn infinite geometric progression is either divergent or convergent.Īn infinite arithmetic progression is always divergent. Geometric Progression vs Arithmetic Progression But when |r| ≥ 1, then the terms become larger and larger infinitely and hence we cannot determine the sum in this case. This is because when the common ratio is less than 1 (a proper fraction), the terms become smaller and smaller as we go forward and they are equivalent to 0. Subtracting equation (2) from equation (1), Proof of Sum of Infinite Geometric Progression FormulaĬonsider an infinite geometric sequence a, ar, ar 2. and the sum of the first n terms, in this case, S n = a + a + a +. If r = 1, the progression looks like a, a, a. Since (r - 1) is in its denominator, it is defined only when r ≠ 1. Subtracting equation (1) from equation (2), Proof of Sum of Finite Geometric Progression FormulaĬonsider a finite geometric progression of n terms, a, ar, ar 2. If the number of terms in a geometric progression is infinite, then the sum of the geometric series is calculated by the formula: If the number of terms in a geometric progression is finite, then the sum of the geometric series is calculated by the formula: As we read in the above section that geometric progression is of two types, finite and infinite geometric progressions, hence the sum of their terms is also calculated by different formulas. The geometric progression sum formula is used to find the sum of all the terms in a geometric progression. is an infinite series where the last term is not defined. It is the progression where the last term is not defined.

Infinite geometric progression contains an infinite number of terms. It is the progression where the last term is defined. Finite geometric progressionįinite geometric progression contains a finite number of terms. Let us see the information about each of these. The geometric progression is of two types. To find the terms of a geometric series, we only need the first term and the constant ratio. The common ratio can have both negative as well as positive values. where 'a' is the first term and 'r' is the common ratio of the progression. The GP is generally represented in form a, ar, ar 2. Columbia University.A geometric progression is a special type of progression where the successive terms bear a constant ratio known as a common ratio. “Private tutoring and its impact on students' academic achievement, formal schooling, and educational inequality in Korea.” Unpublished doctoral thesis.

Geometric sequence formula sn professional#
Tutors, instructors, experts, educators, and other professionals on the platform are independent contractors, who use their own styles, methods, and materials and create their own lesson plans based upon their experience, professional judgment, and the learners with whom they engage. Varsity Tutors connects learners with a variety of experts and professionals. Varsity Tutors does not have affiliation with universities mentioned on its website. Media outlet trademarks are owned by the respective media outlets and are not affiliated with Varsity Tutors.Īward-Winning claim based on CBS Local and Houston Press awards. Names of standardized tests are owned by the trademark holders and are not affiliated with Varsity Tutors LLC.Ĥ.9/5.0 Satisfaction Rating based upon cumulative historical session ratings through 12/31/20.


 0 kommentar(er)
0 kommentar(er)
